Contagens de Borda

Figura 1: Boletim de voto preferencial

Em sistemas democráticos, a escolha de um método eleitoral adequado é crucial para garantir uma representação justa das preferências dos eleitores. Entre os diversos sistemas de votação preferencial, o método de Contagem de Borda destaca-se pela sua simplicidade e pela forma como pondera as diferentes posições nas preferências dos eleitores. Originalmente proposto por Jean-Charles de Borda no século XVIII, este método permite que cada votante classifique os candidatos, atribuindo-lhes pontos de acordo com a posição em que são colocados.
Ao longo do tempo, surgiram várias variantes deste método, que utilizam diferentes esquemas de pontuação para refletir com mais precisão a intenção dos eleitores em contextos específicos. Essas variantes permitem ajustes na forma como as preferências são ponderadas, tornando o método mais flexível para diferentes tipos de eleições.

Problema introdutório (encontrado aqui)

Figura 2: Resultados da votação preferencial entre os candidatos D, S e F.

Errata

No enunciado da questão 2.4. deve-se trocar Silva por Ferreira.

Proposta de resolução

Supondo que o vector eleitoral é \(\left(3,2,1\right)\), a distribuição dos pontos pelo candidato Ferreira foi:

• 32% dos votantes atribuíram 1 ponto;
• 34% dos votantes atribuíram 2 pontos;
• 34% dos votantes atribuíram 3 pontos.

Assim, em média, o candidato Ferreira obteve 2,02pts/votante:

\[\overline{p}=0,32\times 1 +0,34\times 2+ 0,34\times3 = 2,02\; \text{pontos}/votante\]

p <- c(1,2,3)
q <- c(0.32,0.34,0.34)
sum(p*q)

[1] 2.02

Como o candidato Ferreira obteve um total de \(606\) pontos,

\[\#votantes\;=\dfrac{606\;pts}{2,02\;pts/votante}=300.\]

Estes \(300\) votantes são \(60\%\) do total de eleitores inscritos (sócios). Logo, \(\#sócios=\dfrac{300}{0,6}=500. \quad\square\)

Vectores Eleitorais

O método da Contagem de Borda utiliza aquilo a que podemos designar de Vector Eleitoral. No problema acima, o vector eleitoral utilizado foi \(\left(3,2,1\right)\), mas o resultado manter-se-ia inalterado se tivéssemos utilizado o vector eleitoral \(\left(12,8,4\right)\), por exemplo, ou \(\left(1,\frac{2}{3},\frac{1}{3}\right)\), ou ainda \(\left(2,1,0\right)\).

Numa eleição com \(n\) candidatos, o vetor \(P = \left(p_1,p_2, \ldots, p_{n-1},0\right)\) designa-se por vetor eleitoral e estabelece a pontuação que cada eleitor atribui aos candidatos de acordo com a ordem de preferência por si estabelecida: \(p_1\) pontos ao candidato preferido, \(p_2\) pontos ao segundo candidato preferido, e assim sucessivamente, com \(p_1\geq p_2\geq \ldots \geq p_{n-1}\geq 0\) e \(p_1 > 0\).

O caso especial do vector eleitoral \(P_1=\left(1,0,0, \ldots, 0\right)\) corresponde ao método de votação da Pluralidade (maioria simples). Claro que o vector eleitoral \(P_2=\left(k,0,0, \ldots, 0\right)\), com \(k>0\), não iria alterar o resultado da eleição! Podemos dizer, por isso, que \(P_1\) e \(P_2\) são vectores eleitorais equivalentes: \(P_1\equiv P_2\).

Dois vetores eleitorais \(U=\left(u_1,u_2, \ldots, u_{n-1},0\right)\) e \(V = \left(v_1,v_2, \ldots, v_{n-1},0\right)\) dizem-se equivalentes, \(U\equiv V\), se produzem o mesmo resultado numa eleição preferencial, isto é, se a ordenação final dos candidatos se mantém.

Sejam \(U\) e \(V\) vetores eleitorais tais que \(U = kV\), com \(k>0\). Então, \(U\equiv V\).

\(\left(u_1,u_2, \ldots, u_{n-1},0\right) = k \left(v_1,v_2, \ldots, v_{n-1},0\right) \Longrightarrow \left(u_1,u_2, \ldots, u_{n-1},0\right) \equiv \left(v_1,v_2, \ldots, v_{n-1},0\right)\).

Exemplos

• Contagem de Borda (5 candidatos): \(\left(4,3,2,1,0\right)\equiv \left(1,\frac{3}{4},\frac{2}{4},\frac{1}{4},0\right)\)

borda = [x for x in reversed(range(5))]
bordaNormalizado = [round(x/4,2) for x in borda]
print(f'Borda Normalizado: {bordaNormalizado}')

Borda Normalizado: [1.0, 0.75, 0.5, 0.25, 0.0]

• Campeonato de Fórmula 1: \(\left(10,8,6,5,4,3,2,1,0,\ldots,0\right)\equiv \left(1,\frac{8}{10},\frac{6}{10},\frac{5}{10},\frac{4}{10},\frac{3}{10},\frac{2}{10}, \frac{1}{10},0,\ldots,0\right)\)

#lista1 = list(range(8,10,-1))
formula1 = [10,8]+[x for x in range(6,0,-1)]+[0,0,0]
print(f'F1 Normalizado: {[round(x/10,2) for x in formula1]}')

F1 Normalizado: [1.0, 0.8, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.0, 0.0, 0.0]

• Festival Eurovisão da Canção¹: \(\left(12,10,8,7,6,5,4,3,2,1,0,\ldots,0\right)\)

¹ Pontuação atribuída pelo júri internacional. Depois de 2016 o voto popular foi introduzido, mas não é considerado aqui.

#lista1 = list(range(8,10,-1))
eurovisao = [12,10]+[x for x in range(8,0,-1)]+[0,0,0]
print(f'Eurovisão Normalizado: {[round(x/12,2) for x in eurovisao]}')

Eurovisão Normalizado: [1.0, 0.83, 0.67, 0.58, 0.5, 0.42, 0.33, 0.25, 0.17, 0.08, 0.0, 0.0, 0.0]

A contagem de Borda em Nauru

A República de Nauru é provavelmente o Estado independente mais remoto do mundo, uma porção de coral erguido numa vasta e vazia extensão do Oceano Pacífico central. Situada a Sul do equador, é constituída por uma única massa de terra, a ilha de Nauru, um afloramento de baixa altitude com apenas \(21\,km^2\) e uma população total de 9692 pessoas (censo de 2018) de origem predominantemente polinésia.

Figura 3: República de Nauru

Com uma história colonial invulgar, Nauru foi governada por três potências coloniais diferentes: Alemanha, Grã-Bretanha e Austrália. A 31 de janeiro de 1968, Nauru tornou-se um Estado independente, tornando-se assim um dos primeiros Estados insulares do Pacífico a conquistar a independência.

O sistema eleitoral adotado em 1971, uma forma de contagem de Borda, conhecida como contagem de Dowdall Borda, utiliza uma forma única de voto preferencial. Este sistema substituiu o sistema de voto alternativo herdado da Austrália aquando da independência. Os eleitores devem indicar uma ordem de preferência por todos os candidatos no seu boletim de voto. Durante a contagem dos votos, é atribuído a cada preferência um valor correspondente à sua fração de voto. Veja o Guia de Votação de 2022.

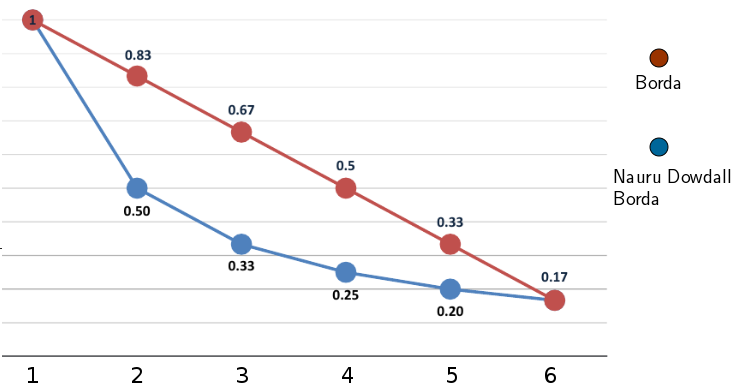
O sistema Dowdall Borda nauruano é ligeiramente mais maioritário do que um sistema Borda puro, uma vez que atribui menos peso às preferências secundárias e inferiores, pois parte do princípio de que os eleitores se preocupam mais com as suas preferências de ordem superior do que com as inferiores, embora estas tenham um impacto nos resultados.

Figura 4: Comparativo das pontuações nas contagens de Borda e Dowdall Borda de Nauru.
Imagem retirada do Relatório de 2022, pág. 13.

Exemplo real em Nauru (círculo de Boe)

Veja-se a ata dos resultados no círculo eleitoral de Boe nas eleições de 2022:

---

Por defeito, na aplicação abaixo a pontuação é a definida pelo método Dowdall Borda usada em Nauru. Pode ajustar os pontos das preferências de cada candidato na barra lateral e ver como isso afeta a classificação final. A simulação com a contagem “clássica” de Borda \(\left(6,5,4,3,2,1\right)\) é particularmente interessante, pelas razões mencionadas na Figura 4 e toda a discussão anterior. Experimente também vectores eleitorais equivalentes ao de Borda clássico para verificar que a ordenação final se mantém.

Laboratório…

---

//md`##### Resultados da contagem de Borda`
md`
| Candidatos                  | Pontuação Total |
|----------------------------|----------------:|
${results.map(d => `| ${d.name} | ${d.total.toFixed(3)} |`).join('\n')}
`

md`##### Pontos`

viewof firstPlacePoints = Inputs.range([0, 6], {value: 1.000, label: "1ª preferência", step: 0.001})
viewof secondPlacePoints = Inputs.range([0, 6], {value: 0.500, label: "2ª preferência", step: 0.001})
viewof thirdPlacePoints = Inputs.range([0, 6], {value: 0.333, label: "3ª preferência", step: 0.001})
viewof fourthPlacePoints = Inputs.range([0, 6], {value: 0.250, label: "4ª preferência", step: 0.001})
viewof fifthPlacePoints = Inputs.range([0, 6], {value: 0.200, label: "5ª preferência", step: 0.001})
viewof sixthPlacePoints = Inputs.range([0, 6], {value: 0.167, label: "6ª preferência", step: 0.001})

points = [firstPlacePoints, secondPlacePoints, thirdPlacePoints, fourthPlacePoints, fifthPlacePoints, sixthPlacePoints]

// Dados dos candidatos com os votos por preferência (baseado na tabela fornecida)
candidates = [
  {name: "WAQA, Baron Divavesi", votes: [103, 66, 114, 106, 260, 393]},
  {name: "NAMADUK, Samvic", votes: [8, 154, 333, 243, 184, 120]},
  {name: "DETENAMO, Demsev", votes: [10, 110, 296, 388, 172, 66]},
  {name: "APPI, Asterio", votes: [396, 175, 92, 51, 107, 221]},
  {name: "HUNT, Martin Porkv", votes: [318, 325, 85, 135, 128, 51]},
  {name: "EMIU, Wananganeen Zac", votes: [207, 212, 122, 119, 191, 191]},
]

// Função para calcular a pontuação Borda
function calculateBorda(points, candidates) {
  return candidates.map(candidate => {
    const total = candidate.votes.reduce((sum, count, i) => sum + count * points[i], 0);
    return {name: candidate.name, total};
  }).sort((a, b) => b.total - a.total); // Ordenar por pontuação
}

// Calculamos os resultados com base nos pontos ajustáveis
results = calculateBorda(points, candidates)

// Mostrar os resultados como lista
md`##### Pontuação Total`

bar_plot = Plot.plot({
  y: {
    label: "Pontos",
    grid: true
  },
  x: {
    label: "Candidatos",
    domain: results.map(d => d.name),
    tickFormat: d => d.split(",")[0], // Mostrar só o primeiro nome para simplificação
    tickSize: 0, // Remover a linha do tick
    labelAnchor: "center",
    tickStyle: {fontSize: 16, fontWeight: "bold"} // Aumentar tamanho da fonte dos nomes e em negrito -- mas parece não resultar!!!
  },
  marks: [
    Plot.barY(results, {x: "name", y: "total", fill: "steelblue"}), // Barras verticais
    Plot.text(results, {x: "name", y: "total", text: d => d.total.toFixed(3), dy: -10, fill: "black", fontWeight: "bold", fontSize: 16}), // Texto das pontuações a bold e maior
    Plot.ruleY([0])  // Para a linha zero
  ]
})

---